Next: Some pictures of a Up: A numerical Singular Perturbation Previous: Introduction

The mathematical problem

The model problem we propose is to find the solution of the equation

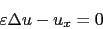$\begin{displaymath} \varepsilon \Delta u - u_x = 0 \end{displaymath}$

(1)

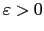for some parameter $\varepsilon >0$ . The equation is defined on the exterior of the unit circle, i.e., on the region

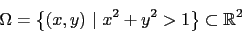$\begin{displaymath} \Omega = \left\{ (x,y) ~\vert~ x^2+y^2 > 1 \right\} \subset \mathbb{R}^2 \end{displaymath}$

(2)

satisfying the boundary conditions

$\displaystyle u(x,y;\varepsilon ) =1$	$\textstyle \mathrm {for}$	$\displaystyle x^2+y^2=1$	(3)
$\displaystyle u(x,y;\varepsilon ) =0$	$\textstyle \mathrm {for}$	$\displaystyle x^2+y^2\to\infty$	(4)