Introduction

In this website we propose a numerical problem and we collect some referencer to results already obtained.

The problem and its analytical solution were described earlier in the paper:
P.W. Hemker, A singularly perturbed model problem for numerical computation. J. Comp. Appl. Math. 76 (1996) 277-285.
(http://repos.project.cwi.nl:8888/cwi repository/docs/I/02/2193A.pdf )

Some earlier numerical solutions have been published by

1. M.H. van Raalte, Multigrid Analysis and Embedded Boundary Conditions for Discontinuous Galerkin Discretization. Thesis University of Amsterdam, 2004.
   (http://homepages.cwi.nl/ pieth/db/mhvraalte-thesis.pdf)
   In particular Chapter 7: A feasibility study for DG discretization with embedded Dirichlet boundary condition.
2. R. Xiaoan and L. Xanthis 'Les fleurs du mal': an adaptive wavelet method of arbitrary lines I: convection-diffusion problems. Comptes Rendus Mecanique, 332 (2004) 23-29.
   (http://dx.doi.org/10.1016/j.crme.2003.10.004)
3. E.D. Havik, P.W. Hemker and W. Hoffmann, Application of the Over-Set Grid Technique to a Model Singular Perturbation Problem. Computing 65 (2000) pp. 339-356
   (http://repos.project.cwi.nl:8888/cwi repository/docs/I/01/1155A.pdf )
4. J. Noordmans and P.W. Hemker, Application of an Adaptive Sparse Grid Technique to a Model Singular Perturbation Problem. Computing 65 (2000) pp. 357-378
   (http://repos.project.cwi.nl:8888/cwi repository/docs/I/01/1154A.pdf)
5. P. Knobloch and L. Tobiska, On bubble-based modifications of the nonconforming P1 element for solving convection-diffusion equations, CD-Rom Proceedings of ECCOMAS 2000 held in Barcelona, September 11-14, 2000, (E. Onate, G. Bugeda and B. Suarez eds), FIB, CIMNE, Barcelona, 2000, 1-20. (pdf-file).
6. P.W. Hemker, The numerical solution of a singular perturbation problem in the domain exterior of a circle. Stichting Mathematisch Centrum. Numerieke Wiskunde, Report NW 11 (1974)
   (http://repos.project.cwi.nl:8080/nl/repository db/all publications/9058)

On this website the numerical problem is described in detail. Further, a suggestion is made on how to represent results, with the aim to facilitate comparison of the different methods. However, particular methods may require different ways for showing particular features.

The only strict requirement for submissions for the prize that will be awarded during the BAIL 2008 Conference, is that errors in the solution are measured by the 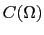$C(\Omega)$-norm !